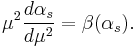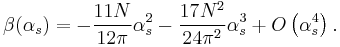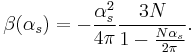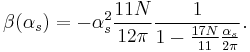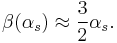Yang–Mills theory
| Yang-Mills theory in the non-perturbative regime:
The equations of Yang–Mills remain unsolved at energy scales relevant for describing atomic nuclei. How does Yang–Mills theory give rise to the physics of nuclei and nuclear constituents? |
| Quantum field theory |
|---|
| History of... |
|
Incomplete theories
|
|
Scientists
Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg • Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Hoodbhoy • Zimmermann • Zinn-Justin
|
Yang–Mills theory is a gauge theory based on the SU(N) group. Wolfgang Pauli formulated in 1953 the first consistent generalization of the five-dimensional theory of Kaluza, Klein, Fock and others to a higher dimensional internal space.[1] Because Pauli saw no way to give masses to the gauge bosons, he refrained from publishing his results formally.[1]
Although Pauli did not publish this theory, he gave talks widely attended by physicists of the time.[2] In early 1954, Chen Ning Yang and Robert Mills [3] developed a modern formulation in an effort to extend the original concept of gauge theory for abelian groups, e.g. quantum electrodynamics, to nonabelian groups to provide an explanation for strong interactions. This initial idea was not a success, since the quanta of the Yang–Mills field must be massless in order to maintain gauge invariance. The massless particles should have long range effects, but these effects are not seen in experiments. The idea was set aside until 1960, when the concept of particles acquiring mass through symmetry breaking in massless theories was put forward, initially by Jeffrey Goldstone, Yoichiro Nambu, and Giovanni Jona-Lasinio.
This prompted a significant restart of Yang–Mills theory studies that proved successful in the formulation of both electroweak unification and quantum chromodynamics (QCD). The electroweak interaction is described by SU(2)xU(1) group while QCD is an SU(3) gauge theory. The electroweak theory is obtained by combining SU(2) with U(1), where quantum electrodynamics (QED) is described by a U(1) group, and is replaced in the unified electroweak theory by a U(1) group representing a weak hypercharge rather than electric charge. The massless bosons from the SU(2)xU(1) theory mix after spontaneous symmetry breaking to produce the 3 massive weak bosons, and the photon field. The Standard Model combines the strong interaction, with the unified electroweak interaction (unifying the weak and electromagnetic interaction) through the symmetry group SU(2)xU(1)xSU(3). In the current epoch the strong interaction is not unified with the electroweak interaction, but from the observed running of the coupling constants it is believed they all converge to a single value at very high energies.
Phenomenology at lower energies in quantum chromodynamics is not completely understood due to the difficulties of managing such a theory with a strong coupling. This is the reason confinement has not been theoretically proven, though it is a consistent experimental observation. Proof that QCD confines at low energy is a mathematical problem of great relevance, and an award has been proposed by the Clay Mathematics Institute for whoever is also able to show that the Yang–Mills theory has a mass gap and its existence.
Contents |
Mathematical overview
Yang–Mills theories are a special example of gauge theory with a non-abelian symmetry group given by the Lagrangian
with the generators of the Lie algebra corresponding to the F-quantities (the curvature or field-strength form) satisfying
and the covariant derivative defined as
where  is the identity for the group generators,
is the identity for the group generators, 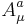 is the vector potential, and
is the vector potential, and  is the coupling constant. In four dimensions, the coupling constant
is the coupling constant. In four dimensions, the coupling constant  is a pure number and for a SU(N) group one has
is a pure number and for a SU(N) group one has 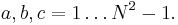
The relation
can be derived by the commutator
The field has the property of being self-interacting and equations of motion that one obtains are said to be semilinear, as nonlinearities are both with and without derivatives. This means that one can manage this theory only by perturbation theory, with small nonlinearities.
Note that the transition between "upper" ("contravariant") and "lower" ("covariant") vector or tensor components is trivial for a indices (e.g. 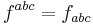 ), whereas for μ and ν it is nontrivial, corresponding e.g. to the usual Lorentz signature,
), whereas for μ and ν it is nontrivial, corresponding e.g. to the usual Lorentz signature, 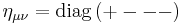 .
.
From the given Lagrangian one can derive the equations of motion given by
Putting 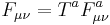 , these can be rewritten as
, these can be rewritten as
A Bianchi identity holds
A source 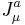 enters into the equations of motion as
enters into the equations of motion as
Note that the currents must properly change under gauge group transformations.
We give here some comments about the physical dimensions of the coupling. We note that, in D dimensions, the field scales as ![[A]=[L^\frac{2-D}{2}]](/2012-wikipedia_en_all_nopic_01_2012/I/18195d0a8d5afb31160d9604b2ef76fa.png) and so the coupling must scale as
and so the coupling must scale as ![\, [g^2]=[L^{D-4}]](/2012-wikipedia_en_all_nopic_01_2012/I/018755fbb08d2a80a0c5e6b0eaedd2e3.png) . This implies that Yang–Mills theory is not renormalizable for dimensions greater than four. Further, we note that, for
. This implies that Yang–Mills theory is not renormalizable for dimensions greater than four. Further, we note that, for 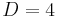 , the coupling is dimensionless and both the field and the square of the coupling have the same dimensions of the field and the coupling of a massless quartic scalar field theory. So, these theories share the scale invariance at the classical level.
, the coupling is dimensionless and both the field and the square of the coupling have the same dimensions of the field and the coupling of a massless quartic scalar field theory. So, these theories share the scale invariance at the classical level.
Quantization of Yang–Mills theory
The most appropriate method to quantize the Yang–Mills theory is by functional methods, i.e. path integrals. One introduces a generating functional for n-point functions as
but this integral has no meaning as is because the potential vector can be arbitrarily chosen due to the gauge freedom. This problem was already known for quantum electrodynamics but here becomes more severe due to non-abelian properties of the gauge group. A way out has been given by Ludvig Faddeev and Victor Popov with the introduction of a ghost field (see Faddeev–Popov ghost) that has the property of being unphysical since, although it agrees with Fermi-Dirac statistics, it is a complex scalar field, which violates the spin-statistics theorem. So, we can write the generating functional as
being
for the field,
for the gauge fixing and
for the ghost. This is the expression commonly used to derive Feynman's rules (see Feynman diagram). Here we have 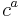 for the ghost field while
for the ghost field while  fixes the gauge's choice for the quantization. Feynman's rules obtained from this functional are the following
fixes the gauge's choice for the quantization. Feynman's rules obtained from this functional are the following
These rules for Feynman diagrams can be obtained when we realize that the generating functional given above can be rewritten as
with
being the generating functional of the free theory. Expanding in  and computing the functional derivatives, we are able to obtain all the n-point functions with perturbation theory. Using LSZ reduction formula we get from the n-point functions the corresponding amplitudes for the given processes and cross sections and decay rates are promptly obtained. The theory is renormalizable and corrections are finite at any order of perturbation theory.
and computing the functional derivatives, we are able to obtain all the n-point functions with perturbation theory. Using LSZ reduction formula we get from the n-point functions the corresponding amplitudes for the given processes and cross sections and decay rates are promptly obtained. The theory is renormalizable and corrections are finite at any order of perturbation theory.
For quantum electrodynamics, where the gauge group is abelian, the ghost field decouples. This can be easily realized when we look at the coupling between the gauge field and the ghost field that is 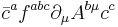 . For the abelian case, all the structure constants
. For the abelian case, all the structure constants 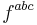 are zero and so there is no coupling. In the non-abelian case, the ghost field appears as a useful way to rewrite the quantum field theory without physical consequences on the observables of the theory as cross sections or decay rates.
are zero and so there is no coupling. In the non-abelian case, the ghost field appears as a useful way to rewrite the quantum field theory without physical consequences on the observables of the theory as cross sections or decay rates.
One of the most important results obtained for Yang–Mills theory is asymptotic freedom. This result can be obtained assuming the coupling constant  is small (so small nonlinearities), as indeed happens to high energies, and applying perturbation theory. The relevance of this result is due to the fact that a Yang–Mills theory that describes strong interaction and asymptotic freedom permits proper treatment of experimental results coming from deep inelastic scattering.
is small (so small nonlinearities), as indeed happens to high energies, and applying perturbation theory. The relevance of this result is due to the fact that a Yang–Mills theory that describes strong interaction and asymptotic freedom permits proper treatment of experimental results coming from deep inelastic scattering.
In order to obtain the behavior of the Yang–Mills theory at high energies, and so to prove asymptotic freedom, one does perturbation theory assuming a small coupling. This is verified a posteriori in the ultraviolet limit. In the opposite limit, the infrared limit, the situation is quite the opposite, as the coupling is too large for perturbation theory to be reliable. Indeed, most of the difficulties that current research meets is just managing the theory at low energies. That is the interesting case, being inherent to the description of hadronic matter and, more generally, to all the observed bound states of gluons and quarks and their confinement (see hadrons). The most used method to study the theory in this limit is to try to solve it on computers (see lattice gauge theory). In this case, large computational resources are needed to be sure the right limit of infinite volume (smaller lattice spacing) is hit. This is the limit the results have to be compared with. Smaller spacing and larger coupling are not independent each other, and larger computational resources are demanded to accomplish both. As of today, the situation appears somewhat satisfactory for the hadronic spectrum and the computation of the gluon and ghost propagators, but the glueball and hybrids spectra are yet a questioned matter in view of the experimental observation of such exotic states. Indeed, the  resonance[4][5] is not seen in any of such lattice computations and contrasting interpretations have been put forward. This is currently a hotly debated issue.
resonance[4][5] is not seen in any of such lattice computations and contrasting interpretations have been put forward. This is currently a hotly debated issue.
Beta function
One of the key properties of a quantum field theory is the behavior over all the energy range of the running coupling. Such a behavior can be obtained from a theory once its beta function is known. Our ability to extract results from a quantum field theory relies on perturbation theory. Once the beta function is known, the behavior at all energy scales of the running coupling is obtained through the equation
being 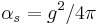 . Yang–Mills theory has the property of being asymptotically free in the large energy limit (ultraviolet limit). This means that, in this limit, the beta function has a minus sign driving the behavior of the running coupling toward even smaller values as the energy increases. Perturbation theory permits to evaluate beta function in this limit producing the following result for SU(N)
. Yang–Mills theory has the property of being asymptotically free in the large energy limit (ultraviolet limit). This means that, in this limit, the beta function has a minus sign driving the behavior of the running coupling toward even smaller values as the energy increases. Perturbation theory permits to evaluate beta function in this limit producing the following result for SU(N)
In the opposite limit of low energies (infrared limit), the beta function is not known. It is note the exact one for a supersymmetric Yang–Mills theory. This has been obtained by Novikov, Shifman, Vainshtein and Zakharov[6] and can be written as
With this starting point, Thomas Ryttov and Francesco Sannino were able to postulate a non-supersymmetric version of it writing down[7]
As can be seen from the beta function of the supersymmetric theory, the limit of a large coupling (infrared limit) implies
and so the running coupling in the deep infrared limit goes to zero making this theory trivial. This implies that the coupling reaches a maximum at some value of the energy turning again to zero as the energy is lowered. Then, if Ryttov and Sannino hypothesis is correct, the same should be true for ordinary Yang–Mills theory. This would be in agreement with recent lattice computations.[8]
Open problems
The Yang–Mills theories were generally acknowledged in the physics community after Gerard 't Hooft, in 1972, could prove their renormalizability. This applies even if the gauge bosons described by this theory are massive, as in the electroweak theory. However, the mass is only an "acquired" one, namely, as suggested, by the famous Higgs mechanism.
Concerning the mathematics, it should be noted that presently, i.e. in 2011, the Yang–Mills theory is a very active field of research, yielding e.g. a classification of differentiable structures of four-dimensional manifolds by Simon Donaldson. Furthermore, the field of Yang–Mills theories was included in the Clay Mathematics Institute's list of "Millennium Prize Problems". Here the prize-problem consists, especially, in a proof of the conjecture that the lowest excitations of a pure Yang–Mills theory (i.e. without matter fields) have a finite mass-gap with regard to the vacuum state. Another open problem, connected with this conjecture, is a proof of the confinement property in the presence of additional Fermion particles.
In physics the survey of Yang–Mills theories does not usually start from perturbation analysis or analytical methods, but more recently from systematic application of numerical methods to lattice gauge theories.
See also
- Yang–Mills existence and mass gap
- Aharonov-Bohm effect
- Coulomb gauge
- Electroweak theory
- Field theoretical formulation of the standard model
- Gauge covariant derivative
- Kaluza-Klein theory
- Lorenz gauge
- Quantum chromodynamics
- Quantum gauge theory
- Symmetry in physics
- Weyl gauge
- Yang–Mills–Higgs equations
References
- ^ a b Straumann, N (2000). "On Pauli's invention of non-abelian Kaluza-Klein Theory in 1953". arXiv:gr-qc/0012054 [gr-qc].
- ^ See Abraham Pais' account of this period as well as L. Susskind's "Superstrings, Physics World on the first non-abelian gauge theory" where Susskind wrote that Yang-Mills was "rediscovered" only because Pauli had chosen not to publish.
- ^ Yang, C. N.; Mills, R. (1954). "Conservation of Isotopic Spin and Isotopic Gauge Invariance". Physical Review 96 (1): 191–195. Bibcode 1954PhRv...96..191Y. doi:10.1103/PhysRev.96.191.
- ^ Caprini, I.; Colangelo, G.; Leutwyler, H. (2006). "Mass and width of the lowest resonance in QCD". Physical Review Letters 96 (13): 132001. arXiv:hep-ph/0512364. Bibcode 2006PhRvL..96m2001C. doi:10.1103/PhysRevLett.96.132001.
- ^ Yndurain, F. J.; Garcia-Martin, R.; Pelaez, J. R. (2007). "Experimental status of the ππ isoscalar S wave at low energy: f0(600) pole and scattering length". Physical Review D 76 (7): 074034. arXiv:hep-ph/0701025. Bibcode 2007PhRvD..76g4034G. doi:10.1103/PhysRevD.76.074034.
- ^ Novikov, V. A.; Shifman, M. A.; A. I. Vainshtein, A. I.; Zakharov, V. I. (1983). "Exact Gell-Mann-Low Function Of Supersymmetric Yang-Mills Theories From Instanton Calculus". Nuclear Physics B 229 (2): 381–393. Bibcode 1983NuPhB.229..381N. doi:10.1016/0550-3213(83)90338-3.
- ^ Ryttov, T.; Sannino, F. (2008). "Supersymmetry Inspired QCD Beta Function". Physical Review D 78 (6): 065001. Bibcode 2008PhRvD..78f5001R. doi:10.1103/PhysRevD.78.065001.
- ^ Bogolubsky, I. L.; Ilgenfritz, E.-M.; A. I. Müller-Preussker, M.; Sternbeck, A. (2009). "Lattice gluodynamics computation of Landau-gauge Green's functions in the deep infrared". Physics Letters B 676 (1-3): 69–73. Bibcode 2009PhLB..676...69B. doi:10.1016/j.physletb.2009.04.076.
Further reading
- Books
- Frampton, P. (2008). Gauge Field Theories (3rd ed.). Wiley-VCH. ISBN 978-3527408351.
- Cheng, T.-P.; Li, L.-F. (1983). Gauge Theory of Elementary Particle Physics. Oxford University Press. ISBN 0-19-851961-3.
- 't Hooft, Gerardus (2005). 50 Years of Yang-Mills theory. World Scientific. ISBN 981-238-934-2.
- Articles
- Svetlichny, George (1999). "Preparation for Gauge Theory". arXiv:math-ph/9902027 [math-ph].
- Gross, D. (1992). "Gauge theory - Past, Present and Future". http://psroc.phys.ntu.edu.tw/cjp/v30/955.pdf. Retrieved 2009-04-23.
External links
|
||||||||
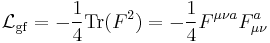
![\ [T^a,T^b]=if^{abc}T^c](/2012-wikipedia_en_all_nopic_01_2012/I/d044180efe4d2925188cdfbfb8d3dc0e.png)
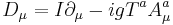
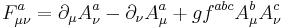
![\ [D_\mu, D_\nu] = -igT^aF_{\mu\nu}^a.](/2012-wikipedia_en_all_nopic_01_2012/I/be8d562970222d1763a85f31e565a842.png)
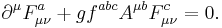
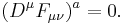
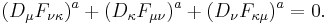
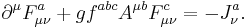
![\ Z[j]=\int [dA]\exp\left[- \frac{i}{4} \int d^4x\operatorname{Tr}(F^{\mu \nu} F_{\mu \nu})%2Bi\int d^4x \, j^a_\mu(x)A^{a\mu}(x)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/c65d395b15fb5f90d6893a356956a332.png)
![\begin{align}
Z[j,\bar\varepsilon,\varepsilon] & = \int [dA][d\bar c][dc] \exp\left\{iS_F[\partial A,A]%2BiS_{gf}[\partial A]%2BiS_g[\partial c,\partial\bar c,c,\bar c,A]\right\} \\
&\exp\left\{i\int d^4x j^a_\mu(x)A^{a\mu}(x)%2Bi\int d^4x[\bar c^a(x)\varepsilon^a(x)%2B\bar\varepsilon^a(x) c^a(x)]\right\}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/d9df2ae25200b00e0ba4db50aa2100eb.png)
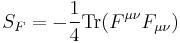
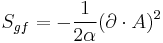
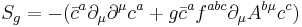
![\begin{align}
Z[j,\bar\varepsilon,\varepsilon] & = \exp\left(-ig\int d^4x \, \frac{\delta}{i\delta\bar\varepsilon^a(x)} f^{abc}\partial_\mu\frac{i\delta}{\delta j^b_\mu(x)} \frac{i\delta}{\delta\varepsilon^c(x)}\right) \exp\left(-ig\int d^4xf^{abc}\partial_\mu\frac{i\delta}{\delta j^a_\nu(x)}\frac{i\delta}{\delta j^b_\mu(x)}\frac{i\delta}{\delta j^{c\nu}(x)}\right)\times \\
& {} \qquad \exp\left(-i\frac{g^2}{4}\int d^4xf^{abc}f^{ars}\frac{i\delta}{\delta j^b_\mu(x)} \frac{i\delta}{\delta j^c_\nu(x)} \frac{i\delta}{\delta j^{r\mu}(x)} \frac{i\delta}{\delta j^{s\nu}(x)}\right)Z_0[j,\bar\varepsilon,\varepsilon]
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/3ef464b37bbd0fbfd9526cc7e5112485.png)
![\ Z_0[j,\bar\varepsilon,\varepsilon]=\exp\left(-\int d^4xd^4y\bar\varepsilon^a(x)C^{ab}(x-y)\varepsilon^b(y)\right)\exp\left(\frac{1}{2}\int d^4xd^4yj^a_\mu(x)D^{ab\mu\nu}(x-y)j^b_\nu(y)\right)](/2012-wikipedia_en_all_nopic_01_2012/I/f0f6ee09610e4059d2d2835156f6346b.png)